lineare Algebra – Vektorrechnung für den Mathe GK

Ich nutze zur besseren Virtualisierung eine 3D Brille mit einem roten und einem blauen Auge. Hier gibt es den Bausatz und den Link zu den benötigten Farben:

Farbfolien Lee 182 (leichtes Rot) und Lee 118 (leichtes Blau)

Thomann LEE 182
Thomann LEE 118

Eine Vorlage für die Brille gibt es hier:

00-AB-3D-Brille

Wie kann man eine blinde Person auf einem Schulhof zu einem Punkt führen? Denkt man über das Problem nach, so verwendet man fast intuitiv Vektoren – ohne zu wissen, dass es Vektoren sind. Schaut mal her.

Hier findet Ihr das Arbeitsblatt „von A nach B“ zum Mannesmann Gymnasium in Duisburg – aber das kann natürlich auch auf andere Schulen übertragen werden.

01-ab-von-A-nach-B

Wenn Ihr Eure Lösungen miteinander vergleicht, findet Ihr in der Regel bereits viele Möglichkeiten, Koordinaten darzustellen. Wir nutzen die kartesische Koordinatendarstellung – bei der die verschiedenen Achsen alle in rechten Winkel zueinander stehen.

Zum Mitzeichnen im Heft habt Ihr hier noch einmal das Arbeitsblatt mit einem Koordinatensystem versehen.

02-ab-erkenntnisse

Mithilfe von Vektoren kann man 3D (und auch 2D, aber das ist langweilig) Objekte beschreiben. Wir fangen mit einem Quader an und steigern uns dann. Versuche erst einmal selber mithilfe der Vorgaben aus dem ersten Teil herauszufinden, welche Koordinaten die übrigen Punkte haben.

Tipp: Bei einem Quader sind alle gegenüberliegenden Strecken gleich lang und parallel ….

03-ab-quader

Probleme? Kein Thema …

Jetzt vesuchen wir mal an einem berühmt berüchtigten Beispiel (das Oktaeder des Grauens) einige neue Erkenntnisse auch selber zu erarbeiten.

Zuerst einmal das Arbeitsblatt, auf dem erst einmal „zum Warmwerden“ etwas alleine gelöst werden soll und dann in Gruppenarbeit Neues erarbeitet werden soll. Gestaffelte Hilfen findet Ihr hier auf der Seite – in einem neuen Format.

04-ab-weiterentwicklung

Wer sich den Quader – der in Wirklichkeit schief im Raum liegt – besser vorstellen möchte. kann das hier machen – einmal ohne und einmal mit 3D Brille.

Die Lösungen und Hilfen findest Du hier:

***

Eine Zusammenfassung an einem etwas einfacherem Beispiel findest Du hier – da kannst Du auch schnell noch Deine Grundlagen üben …

Wie liegen Vektoren denn zueinander? Stehen diese senkrecht oder nicht? Diese Frage lässt sich mithilfe des sogenannten Skalarproduktes schnell beantworten. Das Skalarprodukt habe ich erst einmal nicht hergeleitet.

05-ab-orthogonale-vektoren

Und dann schaue Dir mal meine Erklärung an.

Die bis hierher gelernten Methoden lassen sich super nutzen, um geometrische Figuren (Dreiecke, Vierecke …) zu untersuchen. Man kann manchmal die Fläche berechnen, aber sicher zeigen, ob ein Dreieck rechtwinklig, gleichseitig oder gleichschenklig ist. Ebenso lassen sich Quadrate von Parallelogrammen unterscheiden.

Willst Du Dir lieber selber einmal Gedanken machen, dann sind diese beiden Arbeitsblätter etwas für Dich. Ansonsten erkläre ich auch alles im darauf folgenden Video.

Erarbeite einen Ansatz für die Berechnung der Fläche eines rechtwinkligen Dreiecks

Erarbeite einen Ansatz für die Berechnung der Fläche eines gleichschenkligen Dreiecks

04a-erarbeitung-gleichschenklig

>>>> Klicke hier für eine Hilfe <<<<

Erklärvideo: Wie man mit Flächen umgeht

04a-ab-eigenschaften

Lösungen zum Arbeitsblatt:

Lösung Aufgabe 1)

Lösung Aufgabe 2)

Lösung Aufgabe 3)

Lösung Aufgabe 4)

Lösung Aufgabe 5)

Bist Du schon einmal mit einer Drohne geflogen? Diese können per Fernsteuerung gelenkt werden oder auch vollautomatisch, indem ein Kurs übermittelt wird. ABer was tun, wenn die Verbindung abreist und die Drohne nicht mehr zurückkehrt?

08-ab-gerade-einfuehrung

** Video dazu ***

Nun ist genau das passiert, was natürlich nicht vorkommen darf. Die Drohne fliegt führerlos weiter, bis der Akku leer ist. Nur wo soll man nach ihr suchen?

08-ab-geraden-erarbeitung

*** Video dazu in der Mache***

Rechnen mit Geraden

Alles, was Ihr bisher schon mit Geraden machen konntet, geht natürlich auch mit den hier neu kennengelernten Geraden. Ich lasse mal die Begriffe Punkte einer Geraden und Punktprobe fallen. Im nächsten Arbeitsblatt werden genau diese bereits bekannten Begriffe anhand der altbekannten Geraden wiederholt und dann auf die neuen übertragen.

08-ab-rechnen

Videos zu den beiden Aufgaben

Nachdem wir nun wissen, wie man Geraden erstellt, schauen wir uns mal an, wie diese Geraden im 3D-Raum zueinander liegen können. Hier gibt es die vier Möglichkeiten: identisch, echt parallel, schneiden sich und windschief. Na dann analysiert es malmithilfe dieses Arbeitsblattes:

11-ab-lage-geraden-3D

identische Geraden

echt parallele Geraden

Geraden, die sich schneiden

windschiefe Geraden

Auf einem Flughaben erstellt die Flugsicherung ein aktuelles Bild der Flugzeuge und deren Kurse. Hier eine sicherlich sehr vereinfachte Übungsaufgabe zur VEktorrechnung, bei der Geradengleichungen genutzt werden.

Gerne könnt Ihr diese Aufgaben auch mit einer 3D-Software überprüfen.

Hier erst einmal alle INFOS

220314-INFO-AB-Flugzeuge-am-Flughafen

Wenn Ihr alle Infos gelesen habt, dann versucht doch einmal selber ein Geführ dafür zu bekommen, welche Aufgaben man aus diesen Informationen erstellen kann. Hier einige HInweise für grundlegende Aufgaben:

• Vektor zwischen zwei Punkten, Länge des Vektors
• Länge eines Vektors im Sachzusammenhang (in dem Fall „der Geschwindigkeitsvektoren)
• Neue bzw. alte Position eines Flugzeugs

Aufgaben mit Geradengleichungen

• parallele und senkrechte Geraden
• Puktprobe und Geradengleichungen
• Schnittpunkt zweier Geraden
• Lage zweier Geraden zueinander

Und dann noch einen ganzen Haufen Übungsmaterialien!

220314-AB-Flugzeuge-am-Flughafen

Lösung zu dieser Aufgabe mit Kommentaren und Tipps:

Aus Vorbereitung für die KLausur noch einige weitere Übungen mit Lösungen. Nutze die auf dem AB udn auch uuf direser Seite gegebenen Videos mit 3D Brille, um Dir besser vorstellen zu können, wie man die Aufgaben löst.

13-ab-vermischte-uebungen

Zu dieser Übung gibt es zwei kurze Filme, so dass man sich die Körper besser vorstellen kann.

Lösung zur Aufgabensammlung (mit Lösungsweg):

Lineare Gleichungssysteme haben wir bisher immer nur mit dem GTR gelöst – aber das geht auch „mit der Hand“. Das Verfahren der Wahl heißt Gauß-Alorithmus – nach dem deutschen Mathematiker Carl Friedrich Gauß benannt. Zum Verfahren gibt es sowohl im Internet als auch in jedem Mathebuch unzählige Aufgaben – eine Einführung mit einer Erklärung gibt es hier.

Puh, ganz schön schwierig. In Eurem Mathebuch findet Ihr sicherlich ganz viele Übungsaufgaben zu diesem Thema. Aber hier gibt es auch noch ein Übungsblatt. In dem Übungsblatt findest Du zu jeder Aufgabe einen QR-Code, der Dich zu einer Lösung führt – bei der es auch Kommentare gibt.

13-ab-uebungen-gauss

Die Lösungen zu den jeweiligen Aufgabenteilen (teilweise auch mit Kommentar) findet ihr auf dem Arbeitsblatt über den QR-Code oder eben hier.

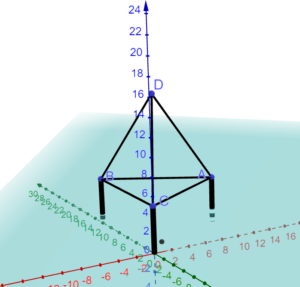
Hast Du Dir schon einmal die Frage gestellt, warum ein Tisch mit vier Beinen ab und an wackelt – also in der Schule gerade in den NW-Räumen wackeln diese Tische ja quasie immer? Wenn DU hingegen zum Beispiel zu Hause einen Tisch besitzt, der nur drei Beine hat, sowackelt dieser gar nicht – kippt allerdings manchmal leichter um.

Du kannst dies gerne mal selber mit zum Beispiel Lego ausprobieren – und schaue Dir dann mein Video an.

Im Video bekommst Du ein paar Aufgaben, die Du mit einem Programm wie zum Beispiel geogebra gut bearbeiten kannst. Diese Aufgaben findest Du noch einmal genauer auf meinem Arbeitsblatt.

14-ab-wackelnder-tisch

Die Videos mit den 3D-Zeichnungen findest Du entweder auf dem Arbeitsblatt oder hier verlinkt.

• dreibeiniger Tisch ohne 3D Brille
• dreibeiniger Tisch mit 3D Brille
• vierbeiniger Tisch ohne 3D Brille
• vierbeiniger Tisch mit 3D Brille

Und warum wackelt der Tisch nun? Wenn Du wirklich keine Idee hast, dann schaue Dir hier diesen Tipp an.

Wow, das ist eine ganze Menge neuer Stoff, schaue Dir mal an, welche Gedanken ich mir gemacht habe.

Du hast sicherlich schon bemerkt, dass es nun um Ebenen und damit auch um Ebenengleichungen geht. Dazu musst Du dein Wissen über Geradengleichungen nur ein kleines bisschen aufwärmen und anwenden und kannst eigentlich schon loslegen.

In diesem Video zeige ich Dir, wie Du eine Ebenengleichung erstellst und wie Du anschließend die Punktprobe durchführst.

Wie auch schon bei Geraden untereinander kann man sich auch fragen, wie eine Gerade nd eine Ebene zueinander liegen können. Dies schauen wir uns jetzt einmal ganz innermathematisch an und üben dabei fleißig den Gauß-Algorithmus.

Auf meinem Arbeitsblatt findest Du drei kombinationen aus Ebene und Gerade, die alle eine andere Lagebeziehung haben. Die Lösungen gibt es diesmal als Lösungsblatt und als kurze Animation. Bitte versuche aber selber auch, mit geogebra sicherer zu werden, da wir in der nächsten Zeit noch viele Anwendungsaufgaben bearbeiten wollen und da ist die Vorstellung gerade wichtig, die hier am besten selbst erarbeitet wird.

xx-ab-lage-ebenen

Zu Beginn musst Du Punkte auf der Gerade / Ebene finden, um einfacher eine der Figuren in geogebra zu zeichnen. Schaue Dir an, wie das geht, wenn Du nicht weiter weißt.

Und dann hier noch einmal die drei Videos, in denen Du die 3D-Animationen sehen kannst.

Abschließend hier noch alle rechenrischen Lösungen.

16-lsg-gerade-ebene

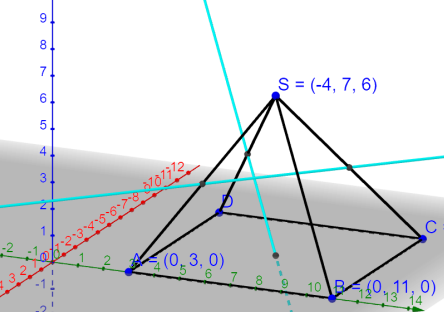
Ich versuche mich mal als Künstler im Duisburger Rheinpark … und Ihr rechnet mal rum …

Im Unterricht bespreche ich mit Euch erst einmal, wie man denn den Schatten meines Tetraeders konstruieren kann, später findet Ihr ganz viele Übungsaufgaben – und wie immer auch die Lösungen dazu.

17-ab-klausur

Im Arbeitsblatt befinden sich bereits die Links zu den 3D Zeichnungen – die Ihr aber eigentlich selber erstellen sollt.

Hier meine fertigen Videos:

Und abschließend dann noch alle Lösungen – aber versucht es erst einmal alleine … in der Klausur gibts die ja schließlich auch nicht …

Wie immer gibt es auch eine Übung zum hilfsmittelfreien Teil. Beachte bitte, dass Du gerne alle Quadratzahlen auswendig lernen könntest …

18-ab-gtr-teil

Und die Lösung gibt es natürlich gleich dazu!