Dreieckkonstruktionen spielen in der Geschichte der Mathematik eine wichtige Rollen. Man erinnere sich nur an den „Satz des Pythagoras“, den vielleicht nicht mehr jeder kennt aber von dem jeder schonmal gehört hat. Bevor man Winkel und Driecke rechnerisch bearbeiten kann (dazu benötigt es nämlich leider einen Taschenrechner), wird in der Scuhle erst einmal mithilfe von Dreiecken konstruiert. Hier kann man neben tollen (auch komplizierten) Anwendungsaufgaben auch dynamische GEometriesoftware nutzen und vertrackte Beweise untersuchen.
1) Was sind kongruente Dreiecke?
Schaue Dir doch einmal dieses Arbeitsblatt an und versuche zu bescreiben, wie die ganzen Dreiecke aus dem Ursprungsdreieck oben links entstanden sind.
Diese Dreiecke sind alle kongruent, dass bedeutet, dass sie eigentlich alle gleich sind. Vom Ursprungsdreieck wurden die kongruenten Dreiecke gedreht, gespiegeln an der Gerade und gespiegelt am Punkt.
2) Die Kongruenzsätze – Dreiecke zeichnen
Es gibt vier Kongruenzsätze, die Du benötigst, um Dreiecke zu konstruieren. Es gibt:
- SSS – drei Seiten gegeben
- SWS – zwei Seiten und den Winkel dazwischen
- SSW – zwei Seiten und ein Winkel, der nicht dazwischen liegt
- WSW – Eine Seite mit zwei benachbarten Winklen
Schaue Dir meine Videos zum Thema an:
Dreieckskonstruktion SSS
Dreieckskonstruktion SWS
Dreieckskonstruktion SSW
Dreieckskonstruktion WSW
Und am Ende noch eine Profiaufgabe:
Es ist gegeben, dass und . Konstruiere das entsprechende Dreieck und finde dessen Besonderheit!
3) Exkurs – Dreiecke sind Stabil, Vierecke nicht
Dreiecke sind im Gegensatz zu Vierecken formstabil – das bedeutet, dass sie sich nicht zur Seite kippen lassen. Daher haben Regale auf der Rpckseite eine Kreuzverspannung und daher hält Euer Kleiderschrank auch erst dann, wenn er eine Rückwand hat. Schaut Euch das mal an!
4) Probleme lösen mit Dreiecken
Dreiecke braucht man ständig zum Lösen von mathematischen Problemen – hier habt Ihr ein paar Anwendungsbeispiele.
Und für die Fortgeschrittenen noch etwas zum Weiterdenken.
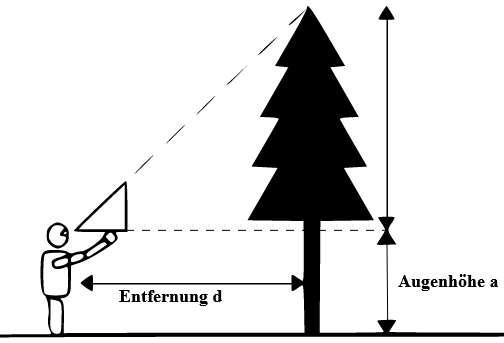
Förster benutzen beim Baumfällen ein sogenanntes „Försterdreieck“ – ein gleichschenkliges Dreieck mit zwei Basiswinkeln von 45 °. Die Benutzung dieses Dreiecks sehr Ihr hier. Erkläre mal, was man mit diesem Dreieck anfangen kann und warum das Konzept so „genial“ ist.
Mit diesen Aufgaben haben viele Schülerinnen und Schüler so ihre Probleme, daher habe ich noch ein paar Beispiele mehr produziert, so dass Ihr Euch diese noch einmal ansehen könnt.
Hier sehr Ihr, wie ein Seefahrer die Höhe einer Klippe mit diesen Dreiecksätzen bestimmen kann.
5) Mittelsenkrechte und Winkelhalbierende
6) Zeichnen mit geogebra
Geogebra ist ein kostenloses und sehr mächtiges Tool, mit dem man (auch dynamische) geometrische Zeichnungen erstellen kann. Ebenso kann man 3D-Zeichnungen konstruieren und auch animieren. Es lohnt sich, damit einmal gearbeitet zu haben. Eigentlich ist das Programm selbsterklärend, aber ein wenig Hilfe schadet ja nie …
Nun ist Euer Auftrag, erst einmal die bereits bekannten Dreiecke zu zeichnen, um das bekannte Wissen anzuwenden. Dazu habe ich Euch ein kleines AB erstellt.
Falls Du ein paar Tipps brauchst (keine Lösungen, es sind nur „Tipps“), dann schaue mal hier nach!
7) Linien am Kreis
Am Kreis gibt es einige „spezielle“ Linien am Kreis. Diese habe ich Euch hier einmal auf einem Arbeitsblatt dargestellt. Bearbeitet es – ich denke, dass Du auch gut einen Vortrag vorbereiten kannst.
8) das Sehnenviereck und seine Eigenschaften
Ein Sehenviereck ist ein ganz besonderes Viereck, das einige recht interessante und ungewöhnliche Eigenschaften hat. Hieran kann man gut das logische Denken schulen und geometrische Beweise üben.
Wenn Du ein paar Tipps brauchst, dann findest Du diese auf dem Arbeitsblatt oder auch hier:
Und nun beweise bitte:
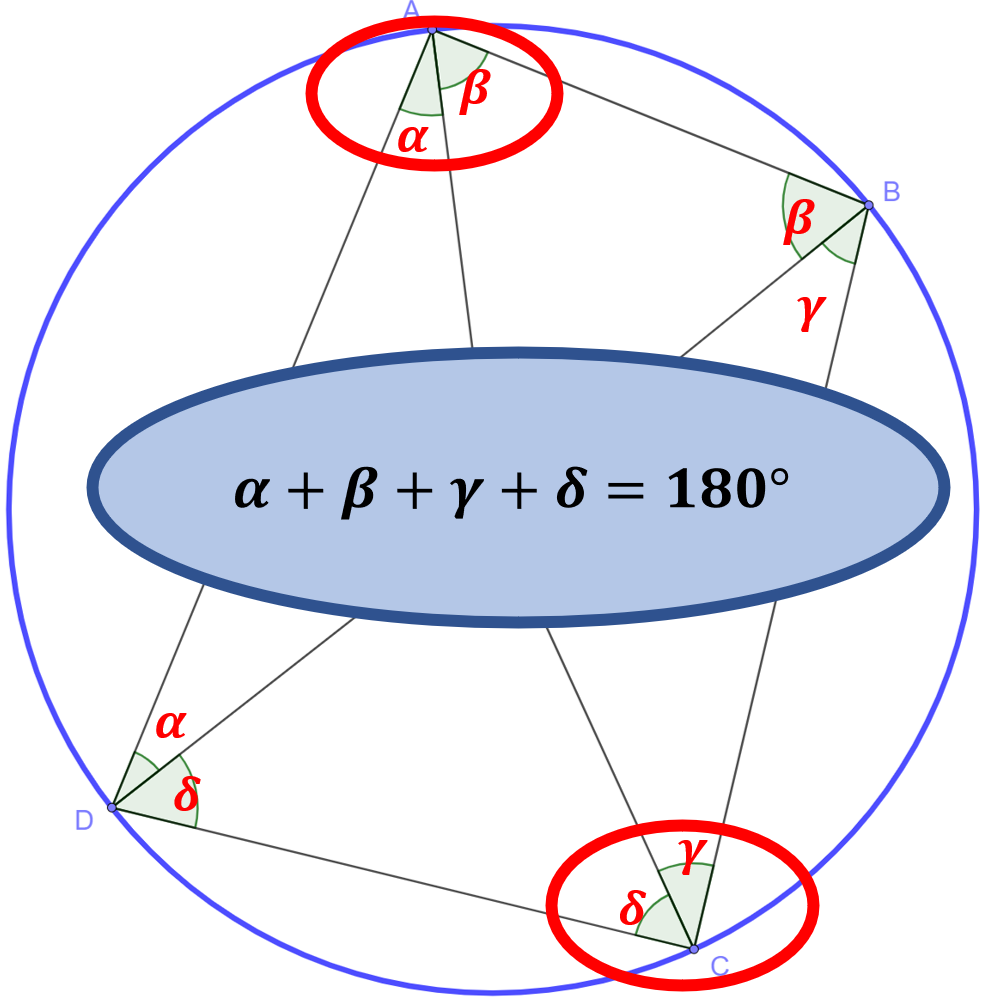
Zeige mir, dass die Summe der gegenüberliegenden Winkel eines Sehenevierecks immer 180° groß sind.
9) Mittelpunktwinkel und Umfangswinkel beim Sehnendreieck
Weitere Winkel, an denen man wirklich gut logisches Argumentieren üben kann, sind der Umfangswinkel und der Mittelpunktwinkel bei einem Sehnendreieck.
Beweise nun diesen Satz:
Der Mittelpunktwinkel eines Sehnenvierecks ist doppelt so groß wie der Umfangswinkel.
2001 total views , 1 views today
Sehr interessant, sehr schön
Find ich gut. Gefällt mir.
Gute Videos, aber die 7d(iamantisch) ist besser
Tolle Videos, aber die 7d(iamantisch) ist besser
Fresh from the garden