
1) Die Bedeutung der Fläche unter einer Funktion im Sachzusammenhang
Bisher haben wir uns mit Funktionswerten und der Steigung einer Funktion auseinandergesetzt – nun schauen wir nach weiteren Einsatzmöglichkeiten. Als Einstiegsbeispiel analysiere ich mit Euch eine sehr einfache „Funktion“, in der die Geschwindigkeit eines Fahrzeugs in Abhängigkeit von der Zeit dargestellt wird. Schaut es Euch mal an!
2) die Stammfunktion zur Berechnung der Fläche
Nun gibt es neben den im ersten Punkt gezeigten „Funktionen“ noch ganzrationale Funktionen zweiten bis vierten Gerades, von denen wir auch eine Fläche unter der Funktion berechnen müssen. Dazu benötigen wir eine sogenannte Stammfunktion und hier schauen wir uns mal an, wie man an diese kommt.
Die Herleitung führe ich erst einmal an Beispielen durch, später gibt es aber auch einen handfesten Beweis, der einmal angeschaut aber auch selber durchgeführt werden kann. Versuche es doch einmal!
Selbstredend gelten die im letzten Video gezeigten Sätze und sind auch richtig, aber wie ist man drauf gekommen?
Und nun berechnen wir eine Fläche unter einer Funktion
Legen wir doch einmal mit einer linearen Funktion los, bei der wir die Fläche sowohl „klassisch“ als auch mithilfe einer Stammfunktion berechnen können. Die Erkenntnisse nehmen wir dann mit und rechnen damit dann auch bei komplexeren Funktionen weiter.
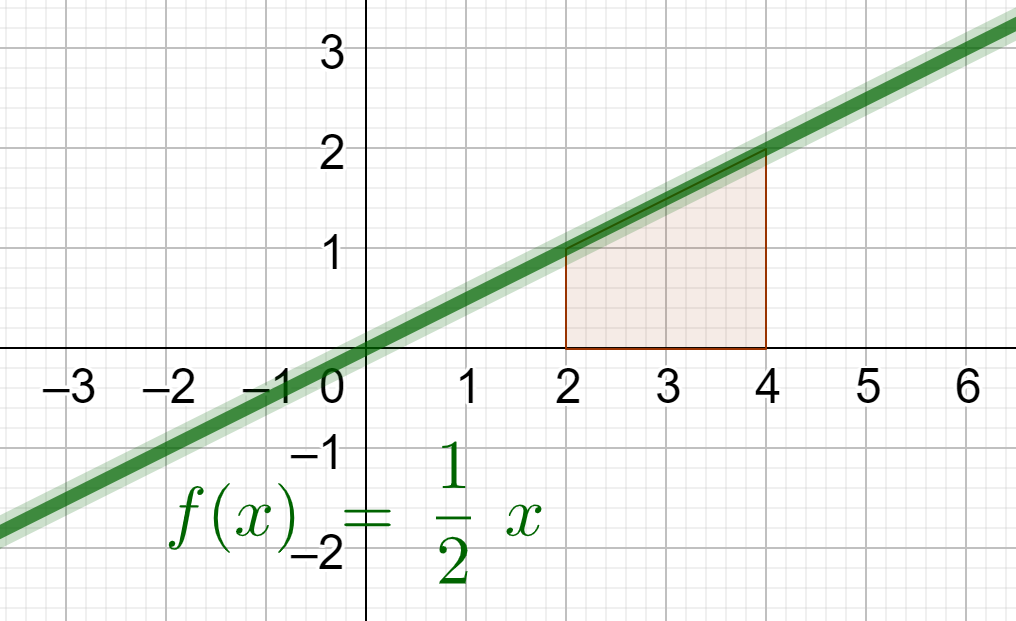
Überlegt Euch einmal, wie man die rote Fläche unter der gegebenen Funktion f(x)=\frac{1}{2} \cdot x im Bereich von 2 bis 4 berechnen kann – also in Integralschreibweise: \int_{2}^{4}{ \frac{1}{2} \cdot x} \, \mathrm{d}x. Ich zeige das Vorgehen im nächsten Video:
Dann übt mal an diesem Beispiel. Ich suche die folgenden Flächen, ein Bild des Funktionsgraphen sehr Ihr unten:
- \int_{2}^{4}{(-x^2+4x)} \, \mathrm{d}x
- \int_{0}^{2}{(-x^2+4x)} \, \mathrm{d}x
- \int_{0}^{4}{(-x^2+4x)} \, \mathrm{d}x
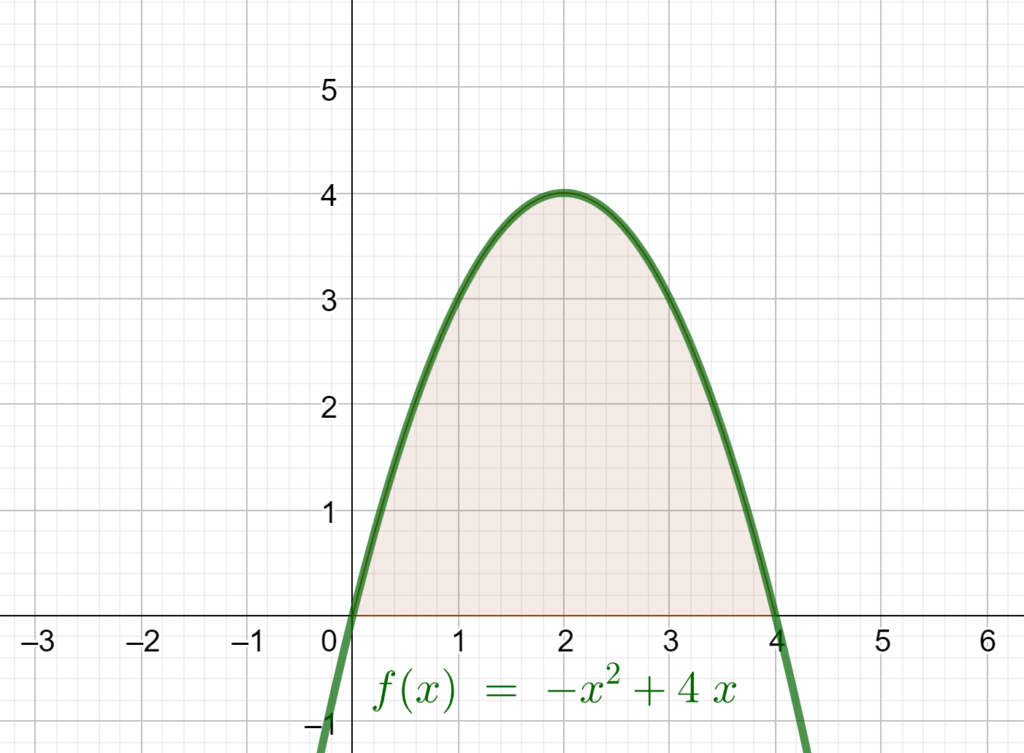
Die Lösungen zu dieser Übung bekommt Ihr dann auch direkt als Video nachgeliefert.
Und jetzt könnt Ihr Euch noch etwas richtig schweres anschauen oder zum nächsten Punkt springen und da fleißig üben.
Ober- und Untersummen
Mithilfe einer Obersumme zeige ich Dir, wie man Stammfunktionen noch herleiten und sogar fachlich richtig beweisen kann. Schaue Dir das einmal am Beispiel für die Funktion f(x)=x² an.
Magst Du es mal selber versuchen? Hier hast Du ein Arbeitsblatt mit allen zu benutzenden Schritten, die jedoch noch in die richtige Reihenfolge gebracht werden müssen. Versuche es doch einmal, eine Lösung findest Du weiter unten.
Und anschließend noch die Lösung meiner Herleitung – zur Abwechslung mal nicht als Video sondern als handgeschriebener Text.
03-lsg-herleitung-x3) Übungen Stammfunktionen und Integrale
Jetzt kann erst einmal geübt werden, lege los. Du findest in Dienem Mathebuch sicherlich ganz viele weitere Übungen, ich belasse es nun einmal bei diesem Arbeitsblatt, bei dem Du eine innermathematische Funktion und auch eine Funktion mit Sachkontext findest.
Ich habe negative Flächen hier zwar schon berechnen lassen, diese aber noch nciht thematisiert, das kommt erst im nächsten Schritt.
04-ab-uebungen-1Die Lösungen dazu gibt es wie immer als kurzes kommentiertes Video.
Lösung zur ersten Übungsaufgabe
Lösung zur zweiten Übungsaufgabe
4) Bedeutung negativer Flächen
Früher hattet Ihr immer dann was falsch gemacht, wenn Ihr für ein Rechteck eine negative Fläche ausgerechnet hattet, denn sowas „komisches“ gab gibts ja nicht. Bei der Integralrechnung, wo die Fläche ja nur ein Mittel zum Zweck im Sachzusammenhang ist, kann eine negative Fläche aber eine ganz erstaunliche Bedeutung haben. Sehr mal her.
negative Flächen innermathematisch
05-ab-negative-flaechenIhr solltet bei diesem Arbeitsblatt herausbekommen:
\int_{0}^{4}{(x^3-6x^2+8x)} \, \mathrm{d}x = 0 mithilfe der Stammfunktion F(x)=\frac{1}{4} \cdot x^4-2x^3+4x
Ihr könnt durch Überprüfen erkennen, dass Flächen unter der X-Achse als negative Flächen interpretiert werden, wenn man diese mithilfe des Integrals berechnet. Wenn Ihr nachrechnet erhälst Du auch wirklich:
- \int_{0}^{2}{(x^3-6x^2+8x)} \, \mathrm{d}x = 4
- \int_{2}^{4}{(x^3-6x^2+8x)} \, \mathrm{d}x = -4
Die Summe dieser beiden Flächen ist dann im übrigen wirklich 0, auch dann, wenn der GTR etwas „anderes“ darstellt.
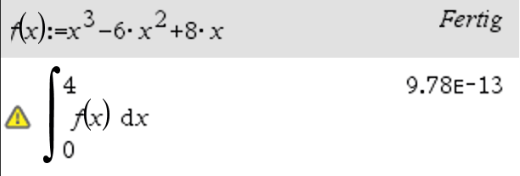
Da der GTR nur näherungsweise rechnet, kommt es hier zu einem so „komischen“ Ergebnis. Wenn Di Dir aber deutlich machst, dass E-13 = 10^{-13} = 0,00000000000001 bedeutet, so erkennst Du, dass es sich um eine wirklich sehr kleine Zahl handelt.
negative Flächen im Sachzusammenhang
Als nächstes versuchen wir, negative Flächen im Sachzusammenhang zu interpretieren. Dazu nutzen wir die gleiche Funktion, die wir auch schon innermathematisch genutzt haben, nur wenden wir auf diese nun einen Sachzusammenhang an.
05-ab-neg-flaechen-szhUm Dich selbst zu prüfen, habe ich ein Quizz erstellt. Arbeite dieses bitte durch!
5) Rechenbeispiele auch im Sachzusammenhang
Jetzt gibt es endlich mal ein paar Aufgaben zum Üben und auch ein bisschen zum Lernen. Diese drei hier haben immer einen Sachzusammenhang und beinhalten alle negative Flächen. Ihr müsst Euch also über die Bedeutung der negativen Flächen im Sachzusammenhang Gedanken machen.
Aufgabensammlung 1
09-ab-uebungen-sachzusammenhangUm mit der ersten Aufgabe etwas „warm“ zu werden hier ein kleines Quizz. Die Funktionsgleichung muss für das Quizz bereits gezeichnet sein (also die Aufgabe a gelöst sein).
Die Lösung zur ersten Aufgabe bekommt Ihr hier als Video, dieses Video hilft auch beim Bearbeiten der anderen beiden Aufgaben, die sich auf dem Arbeitsblatt auf den Seiten 2 und 3 befinden.
Aufgabensammlung 2 – das Flugzeug
Hier hast Du noch eine weitere Aufgabe, die man durchaus auch als Klausuraufgabe nutzen könnte.
xx-ab-uebungsaufgabe-flughafenEine Musterlösung wird noch nachgereicht.
*** Musterlösung*
Aufgabensammlung 3 – der hilfsmittelfreie Aufgabenteil
Und abschließend bekommt Ihr noch eine Aufgabe, die ohne Hilfsmittel zu lösen sein sollte.
xx-ab-hmf-uebungDie Lösung kommt dann hier hin …
6) Grenzen eines Integrals gesucht
Wir können nun gut Integrale berechnen, wenn die Funktion und die Grenzen gegeben sind. Manchmal ist aber auch eine Grenze eines Integrals gesucht.
Von einem Regenwasser-Rückhaltebecken ist die Zufluss- bzw. die Abflussrate gegeben – die in der Aufgabe als Änderungsrate des Beckens bezeichnet wird. Anhand dieses Sachzusammenhangs zeige ich Dir, wie man die Grenzen eines Integrals bestimmen kann.
Um besser arbeiten zu können hast Du hier ein Arbeitsblatt, auf dem alle Informationen und auch der Funktionsgraph zu dieser Einführung gegeben sind.
07-ab-aenderungsrate-regenwasserbeckenUbungsaufgabe 1 (GTR)
Gegeben ist die Funktion f(x)=x^2 +1 . Berechne die obere Grenze, damit die Fläche unter dieser Funktion ab x=0 den Wert 10FE besitzt.
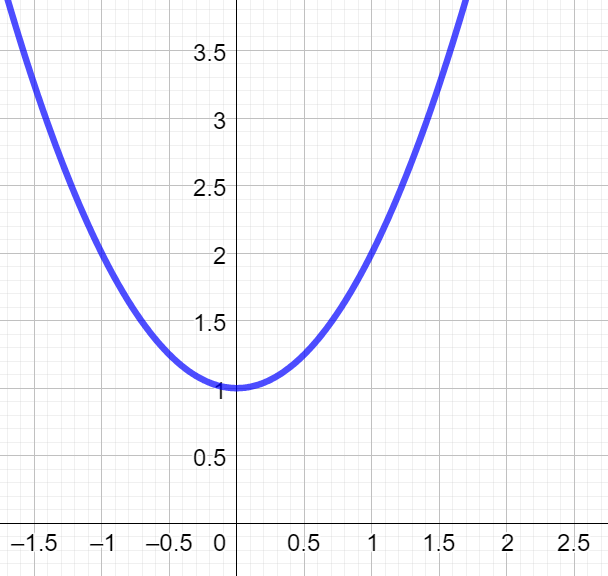
Übungsaufgabe 2 (HMF)
Gegeben ist die Funktion f(x)=0.5 \cdot x +1 . Berechne die obere Grenze, damit die Fläche unter dieser Funktion ab x=2 den Wert 5 FE besitzt.
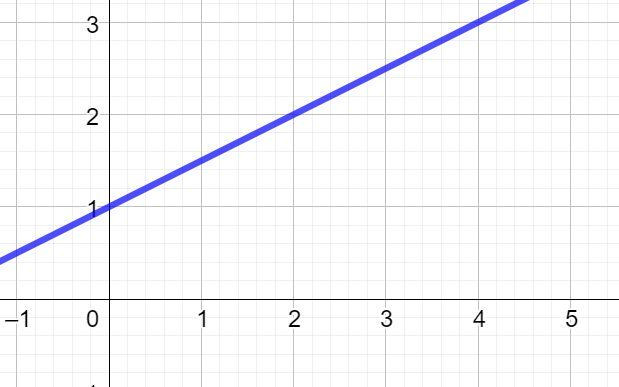
Lösung Aufgabe 1:
Löse diese Term: \int_{0}^{a}{f(x)} \, \mathrm{d}x = 10 mithilfe des GTRs.
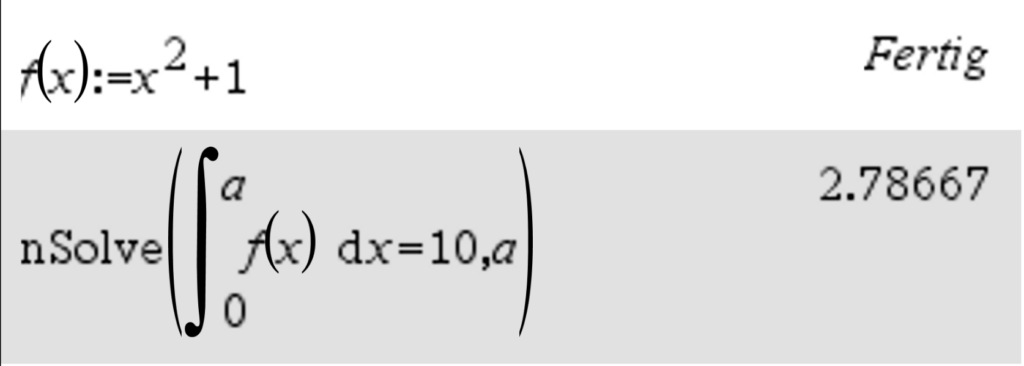
Damit ist die gesuchte Grenze a=2.79.
Lösung Aufgabe 2:
Löse den Term \int_{2}^{a}{0.5x+1} \, \mathrm{d}x = 5, indem Du diesen umformst in:
F(a)-F(2)=14 mit der Stammfunktion F(x)=1/4x^2+1x.
Daraus folgt dann: 1/4 a^2+a-3=5, was Du in eine quadratische Gleichung umformen kannst und dann mit der PQ-Formel lösen kannst.
1/4 a^2+a-8=0 … dann mit 4 multiplizieren
a^2+4 \cdot a - 32 =0 … und dann die PQ-Formel anwenden
a_1 = 4 oder a_2=-8
7) der durchschnittliche Funktionswert
Mithilfe eines Integrals kannst Du den durchschnittlichen Funktionswert einer Funktion in einem bestimmten BEreich berechnen. Hierzu greife ich noch einmal die Funktion aus dem letzten Punkt auf und erläutere dies.
07-ab-aenderungsrate-regenwasserbeckenÜbungsaufgabe:
8) Die Fläche zwischen zwei Funktionen
Bisher haben wir uns nur mit Flächen auseinandergesetzt, die zwischen der Funktion f und der X-Achse gelegen haben. Man kann aber auch Flächen berechnen, die rundherum von Funktionen eingeschlossen sind – wie beispielsweise diese „Medaille“, die von den Funktionen f und h eingeschlossen ist.
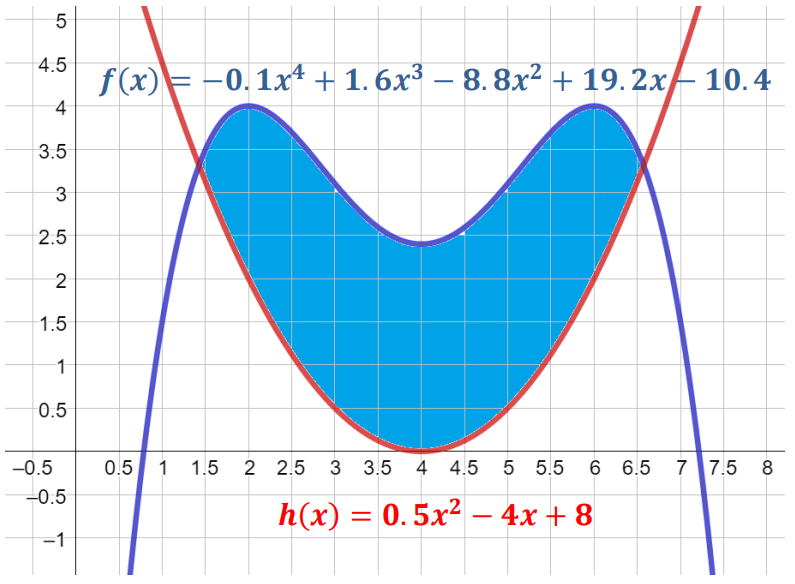
Dann noch ein paar ergänzende Übungen:
Zeige, dass die Funktion f gleich der Funktion k(x)=-0.1\cdot (x-2)^2 \cdot (x-6)^2 +4 ist.
Bestimme die Differenzfunktion d(x)=f(x)-h(x) und zeichne diese mit dem GTR.
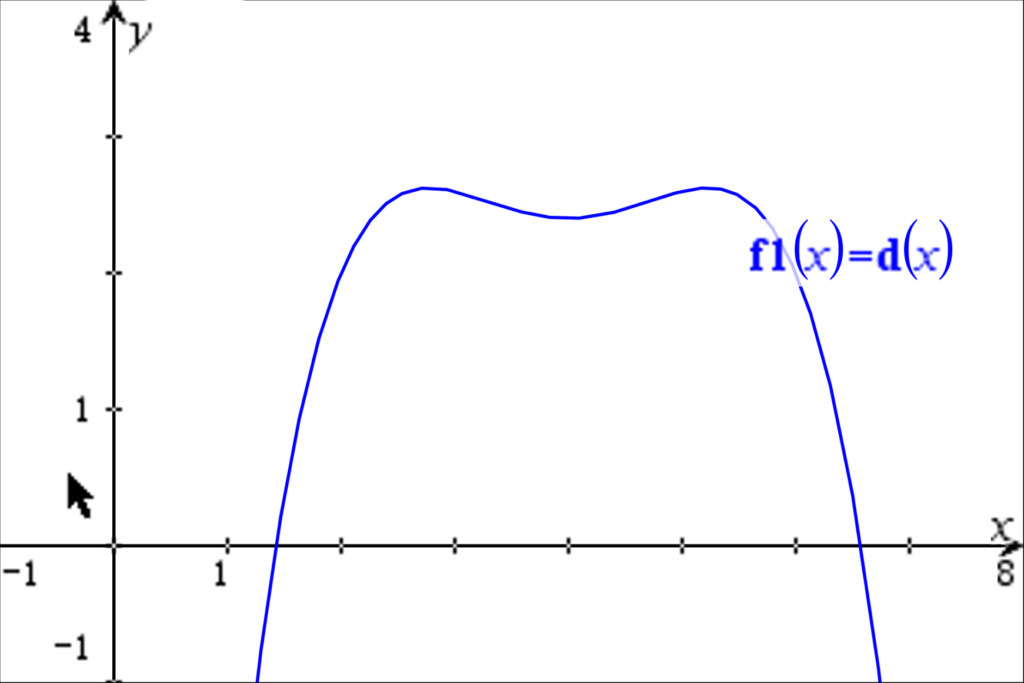
ein Übungsblatt
Bearbeite dieses Übungsblatt.
13-AB-Flaechen-zwischen-zwei-Funktionen-Uebung ![]()