
„Nimm die Geschwindigkeit eines Autos in km/h und teile sie durch 10. Multipliziere das Ergebnis mit sich selbst und Du hast den (zumindest ungefähren) Bremsweg des Autos.“
Diese Formel wirst Du lernen, wenn Du einen Führerschein für ein Auto machen willst. Warum das richtig ist – bzw. wie es dazu kommt – wirst Du im Fach Physik lernen. Aber genau dieser Zusammenhang – zwischen Geschwindigkeit und Bremsweg – ist eben kein linearer oder proportionaler Zusammenhang mehr sondern eine neue Art. Darum geht es nun.
1) Wozu jetzt auch noch quadratische Funktionen?
Vor etwa einem Jahr habt Ihr Euch mit Geraden, den sogenannten linearen Funktionen auseinandergesetzt. Und jetzt geht es damit weiter – nur, dass die Funktionen keine geraden Striche mehr sind. Denn es gibt noch ganz andere Zusammenhänge und folglich auch ganz andere Funktionen.
einige Basisaufgaben zur Wiederholung von Geraden
Will man den Bremsweg eines Fahrzeuges (in dem Fall ist es ein Auto, es kann aber auch ein Fahrrad sein) beschreiben, so kommt man mit linearen Funktionen nicht mehr weit. Erarbeite selber anhand dieses Aufgabenblattes, warum eine lineare Funktion nicht ausreicht, um einen Bremsweg zu beschreiben.
01-ab-bremswegIm Arbeitsblatt befinden sich einige Videos bzw. Hilfen, die gibt es hier noch einmal:
2) die Normalparabel
*** Hier kommt noch etwas hin ***
3) Streckung und Stauchung der Normalparabel
Mit einer Normalparabeln kommt man aber noch nicht sehr weit. Parabelförmige Zusammenhänge sind meistens „irgendwie anders“ wie zum Beispiel der parabelförmige Bremsweg.
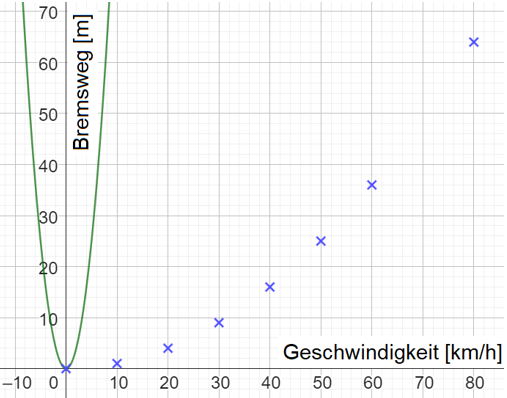
Die Parabel muss also irgendwie verändert werden. Finde selber heraus und beschreibe mithilfe eines Links, wie diese Veränderung erreicht werden kann.
03-ab-streckungsfaktor>>> Link zur geogebra-Datei aus dem Arbeitsblatt. <<<
*** Ein paar Übungsaufgaben und ein Erklärvideo ***
4) Verschiebung der Parabel in X- und Y-Richtung
Verschiebung in Y-Richtung – also nach oben und unten
Strecken und Stauchen alleine reicht leider nicht aus, um die Parabel vollständig flexibel nutzbar zu machen. Sie muss auch noch verschoben werden – und damit beginnen wir erst einmal, indem wir die Parabel in Richtung der Y-Achse verschieben.
04-ab-verschiebung-y>>> LINK zur Geogebra-Datei aus dem Arbeitsblatt <<<
*** Hier kommt noch ein Erklärvideo hin ***
Verschiebung in X-Richtung – also nach links und rechts
04-ab-verschiebung-x*** Hier fehlt noch ein Erklärvideo ***
5) die Scheitelpunktform
Nun sind von Parabeln drei Möglichkeiten bekannt, diese zu verändern:
- Strecken und Stauchen
- Verschieben in Y-Richtung
- Verschieben in X-Richtung
Dies kann nun kombiniert werden und heraus kommt eine Parabel in der sogenannten Scheitelpunktform:
6) Nullstellen berechnen – oder andere Stellen
*** HIER fehlt noch Inhalt …****
7) Umwandlung der Scheitelpunktform in die Normalenform – und zurück
Was soll denn die Normalenform bringen? Schaut Euch an, wozu die Normalenform da ist und wie man eine Parabel in die Normalenform umwandelt.
*** Hier kommt ein Video hin ***
Und wie geht das in die andere Richtung? Ich erkläre es Euch im Video.
Puh, das ist jetzt abe rnicht sooo einfach wie gedacht … macht nichts, hier könnt Ihr Euch noch einmal einige Beispiele anschauen.
8) die Faktordarstellung einer quadratischen Funktion
*** Hier fehlt noch der Inhalt ***
9) die PQ-Formel
Die PQ-Formel gehört in der Sekundarstufe 2 zum normalen Handwerkszeug, wenn Ihr mit ganzrationalen Funktionen arbeiten müsst. Hier werden schon einmal die Grundlagen dazu gelegt.
Wozu braucht man die PQ-Formel eigentlich?
Herleitung der PQ-Formel
Eigentlich ist die PQ-Formel nur eine „Abkürzung“, denn die Nullstelle einer quadratischen Funktion in der Normalenform könnt Ihr ja schon rechnen – indem Ihr die Normalenform einfach in die Scheitelpunktform umwandelt. Nur leider braucht man dies so oft, dass man sich lieber diese Formel hier merkt:
Rechnen mit der PQ-Formel
Einmal für alle zum Anschaeun: Wie man die PQ-Formel an einem komplizierten Beispiel anwendet!
![]()