Dreiecke und Vierecke spielen eine große Rolle in der Mathematik und auch in allen anwendungsorientierten Problemen. Daher widmen wir uns nun den Formeln, mit denen man die Flächeninhalte dieser Formen bestimmen kann.
Du benötigst diese Materialien:
Die Dreiecke mit den Nummern: 1,2,
Die Vierecke mit den Nummern:
1) Eigenschaften von Flächen
Kennst Du noch die Eigenschaften eines Dreiecks oder eines Parallelogramms? Schaue Dir das Video hier an und ordne anschließend die Eigenschaften den verschiedenen Flächen zu, die Du in Deiner Materialsammlung findest.
Auftrag 1:
Finde mithilfe dieses Arbeitsblattes in New York möglichst viele Flächen.
Lade Dir die Datei herunter und arbeite damit.
Auftrag 2:
Ordne die Eigenschaften aus dem Bild den Objekten aus Deiner Materialsammlung zu. Diskutiere die Lösung mit einem Partner. Gerne kann Deine Lösung auch in auf z.B. einem Poster oder in einem eigenen Video dargestellt werden.
Nutze die Hinweise aus der folgenden Datei als Hilfestellung.
Auftrag 3:
Formuliere fertige Beschreibungen für die genutzten Flächen. Diese können gerne in der Darstellung von Aufgabe 2 ergänzt werden.
Nutze die Infos aus der folgenden Datei als Hinfestellung.
2) Eine Formel für rechtwinklige Dreiecke
Rechtwinklige Dreiecke kann man recht einfach nutzen, um mit ihnen eine Formel für Dreiecke herzuleiten – daher beginnen wir damit und werden dann in den nächsten Schritten auch Formeln für allgemeine Dreiecke finden.
Schaue Dir erst einmal mein Video an.
Auftrag 1:
Leite eine Formel für die Fläche des rechtwinkligen Dreieckes 1 her, indem Du die Materialien
- 2 * Dreieck 1
verwendest.
Auftrag 2:
Leite eine Formel für die Fläche des rechtwinkligen Dreiecks 1 her, indem Du die Materialien
- 1 * Dreieck 1
- 1 * Dreieck 2
- 1 * Trapez 1
- 1 * Trapez 2
verwendest. Du kannst die Formel auf zwei verschiedene Arten herleiten.
Auftrag 3:
Leite eine Formel für die Fläche des rechtwinkligen Dreiecks 1 her (die sich aber auf allgemeine Dreiecke verallgemeinern lässt), indem Du
- 1 * Dreieck 1
- 1 * Dreieck 3
- 1 * Dreieck 4
- 1 * Trapez 5
nutzt. Weiterhin benötigst Du für dieses Dreieck die sogenannte „Höhe eines Dreiecks“. Schaue Dir die Info dazu an.
Abschließend kannst Du alle Informationen hier zusammenfassen:
Lösungen findest Du hier:
3) Funktioniert unsere Formel auch für unregelmäßige Dreiecke?
Nun übertragen wir unsere Erkenntnisse auf unregelmäßige Dreiecke.
Rückführung auf rechtwinklige Dreiecke
Versuche das Dreieck 10 mithilfe der Dreiecke 9 und 2 auf die Flächenformel für rechtwinklige Dreiecke zurückzuführen.
Kannst Du (s. Hilfestellung) die Formel herleiten?
Hilfestellung:
Die Höhe eines Dreiecks kann auch außerhalb liegen . schaue Dir auf der verlinkten Datei die zweite Seite an.
Lösungsvideo:
Zerlegung eines unregelmäßigen Dreiecks
Zerlege das Dreieck 10 mithilfe von
- Dreieck 13
- Dreieck 14
- Dreieck 15
- Rechteck 3
und baue diese neu zu einem Rechteck zusammen. Erläutere die bekannte Formel, mit der Du die Fläche eines Dreiecks berechnen kannst.
Hilfestellung:
Die Höhe eines Dreiecks kann auch außerhalb liegen . schaue Dir auf der verlinkten Datei die zweite Seite an.
Lösungsvideo:
Eine kleine Hilfe zur Konstruktion aus dem Video. Gerne kannst Du diese Zeichnung abzeichnen oder kopieren.
Bearbeite dieses Arbeitsblatt, bei dem Du die Flächen von vielen verschiedenen Dreiecken mit dem Schwerpunkt „Höhen finden“ bestimmen musst.
4) Eine Formel zur Berechnung der Fläche von allgemeinen Dreiecken
Nun haben wir endlich eine Formel für die Fläche eines Dreiecks hergeleitet – und müssen damit nur noch ein wenig üben. Bearbeite das Arbeitsblatt.
Zum Zeichnen benötigst Du die Kongruentsätze, mit deren Hilfe man Dreiecke zeichnen kann. Vielleicht musst Du das noch einmal wiederholen. Schaue dazu eine andere Seite an. Die Infos zu den kongruentsätzen findest Du unter Punkt 2.
5) Übungsaufgaben zu Flächen von Dreiecken
Wie berechnet man die Fläche und wie findet man fehlende Strecken?
Auftrag 1: Löse das Arbeitsblatt
Bearbeite die häufig recht innermathematischen Aufgaben des Arbeitsblattes.
*** Hier kommt bald ein Lösungsvideo hin … ***
Auftrag 2: Dreiecke zeichnen wiederholen
Zum Zeichnen von Dreiecken benötigst Du die sogenannten Krongruentsätze, die im letzten Schuljahr Thema waren. Diese musst Du nun sicher können. Schaue Dir – falls noch nciht geschehen, auf der im Bild verlinkten Webseite den Punkt 2 noch einmal an und wiederhole das Zeichnen von Dreiecken mithilfe der Kongruentsätze.
Auftrag 3: Dreiecke aus der Karte
Suche Dir zwei Dreiecke aus der Karte, die zu Beginn der Reihe genutzt wurde. Übertrage diese in Deinen Hefter und berechne anschließend den Flächeninhalt in der Originalen Größe – also in Quadratkilometern.
6) Eine Formel zur Berechnung der Fläche eines Parallelogramms
Als nächstes wird das bei Dreiecken bereits gut geübte Verfahren angewendet, um eine Formel für den Flächeninhalt eines Parallelogramms zu finden.
Auftrag 1:
Nutze das Dreieck 2 sowie das Trapez 1, um eine Formel für das Parallelogramm 1 herzuleiten. Übertrage das Parallelogramm in Deinen Hefter und erläutere Deine Herleitung.
Auftrag 2:
Versuche eine Formel für den Flächeninhalt des Parallelogrammes P1 mithilfe der beiden Dreiecke 20 herzuleiten. Übertrage das Parallelogramm in Deinen HEfter und erläutere die Herleitung.
Auftrag 3:
Übertrage diese Zeichnung eines Parallelogramms in Deinen Hefter und fasse die von Dir gefundene Formel mithilfe der Skizze zusammen.
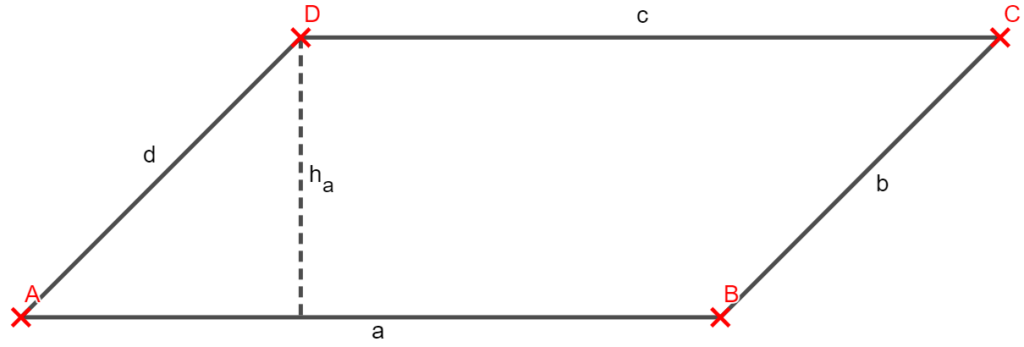
Auftrag 4:
Ich behaupte, dass das grüne und das schwarze Parallelogramm die gleiche Fläche besitzt. Erläutere und begründe!

7) Eine Formel zur Berechnung der Fläche eines rechtwinkligen Trapezes
Als nächstes ist eine Formel für ein Trapez gesucht. Dazu beginnst Du mit dem rechtwinkligen Trapez und untersuchst dann ein allgemeines Trapez.
Auftrag 1:
Finde mithilfe des Fünfecks 2 und des Dreiecks 11 eine Formel, mit deren Hilfe Du die Fläche des Trapezes 1 berechnen kannst. Übertrage die Erklärung zu Deiner Formel in Dein Heft.
Auftrag 2:
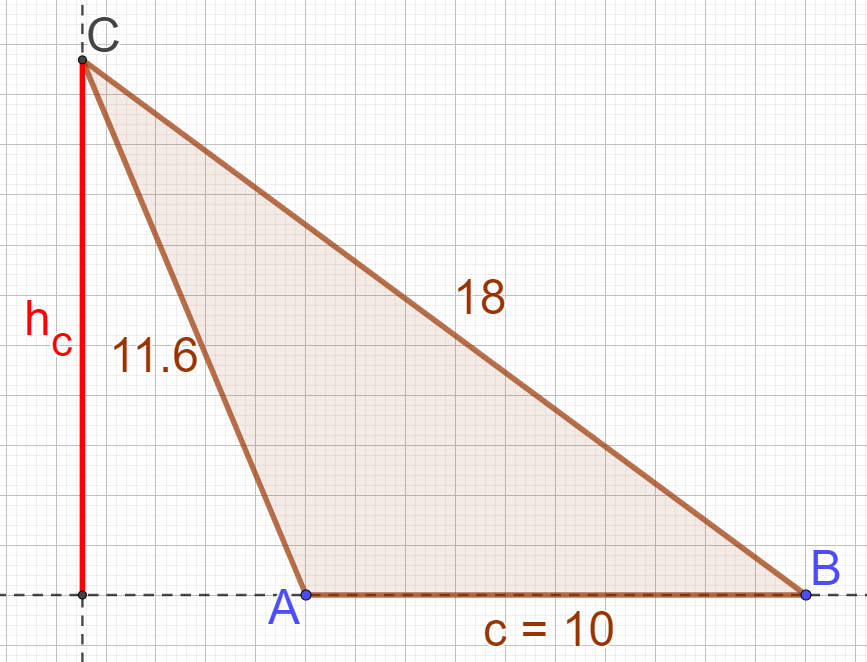
Prüfe diese Formel anschließend anhand des abgebildeten Trapezes auf dieser Seite. Übertrage es ins Heft und bestimme die fehlende Seitenlänge. Rechnest Du richtig, so erhältst Du als Fläche 66 cm².
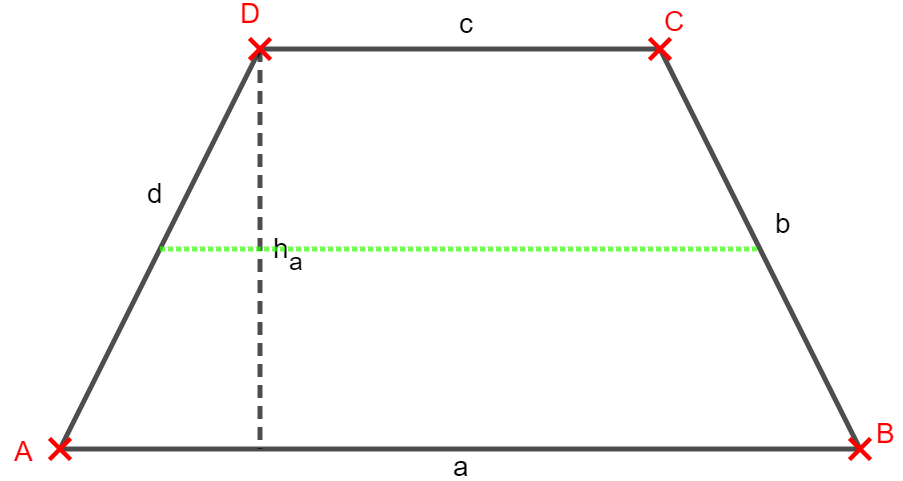
8) Eine Formel für ein allgemeines Trapez
Nun gibt es leider nicht nur rechtwinklige Trapeze sondern auch solche, die man als allgemeine Trapeze bezeichnet. Hier sind nur noch zwei Seiten parallel zueinander.
Auftrag 1:
Finde eine Formel für ein solches allgemeines Trapez 8, indem die Dreiecke 18 und 19 sowie das Fünfeck 3 genutzt wird. Übertrage das Trapez in Dein Heft und sichere dort die Begründung für die Flächenformel.
Auftrag 2:
Prüfe anschließend mithilfe des Trapezes hier Deine Formel. Rechnest Du richtig, so musst
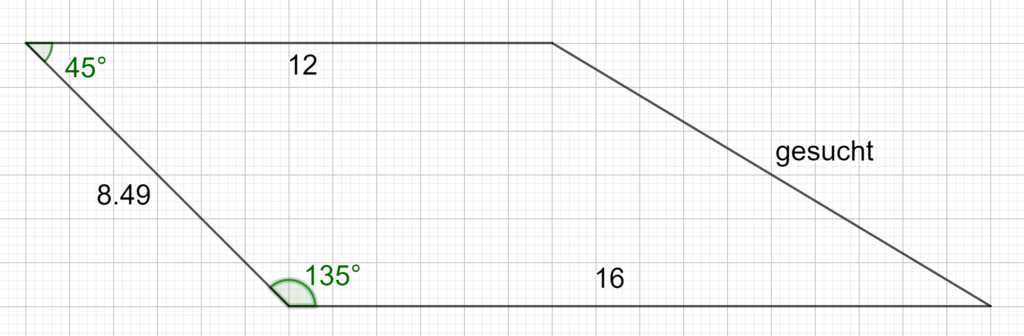
Auftrag:
Übertrage dieses Trapez in Dein Heft und erkläre an ihm, wie die Fläche eines Trapezes berechnet werden kann.
9) Übungsaufgaben zu Parallelogrammen und Trapezen
10) Zusammengesetzte Flächen
Nicht immer treten die Flächen in Reinform auf. Oft sind verschiedene Flächen miteinander kombiniert, so dass man diese erst zerlegen muss.
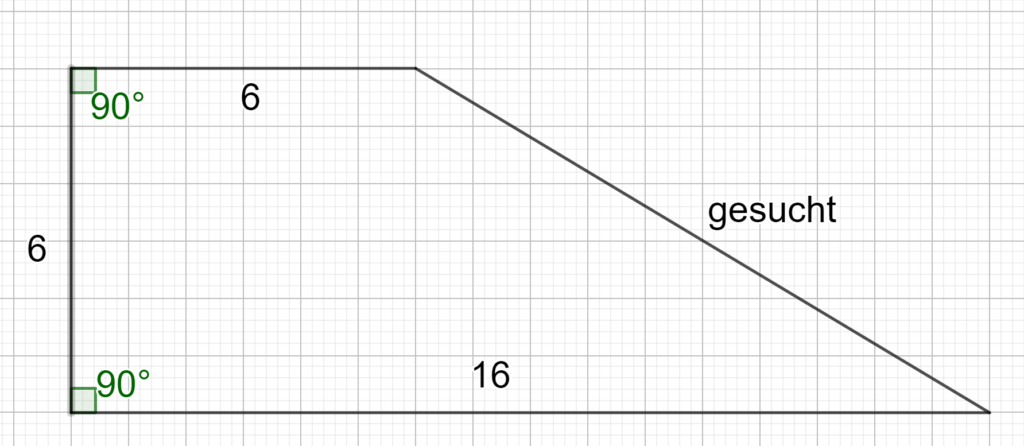
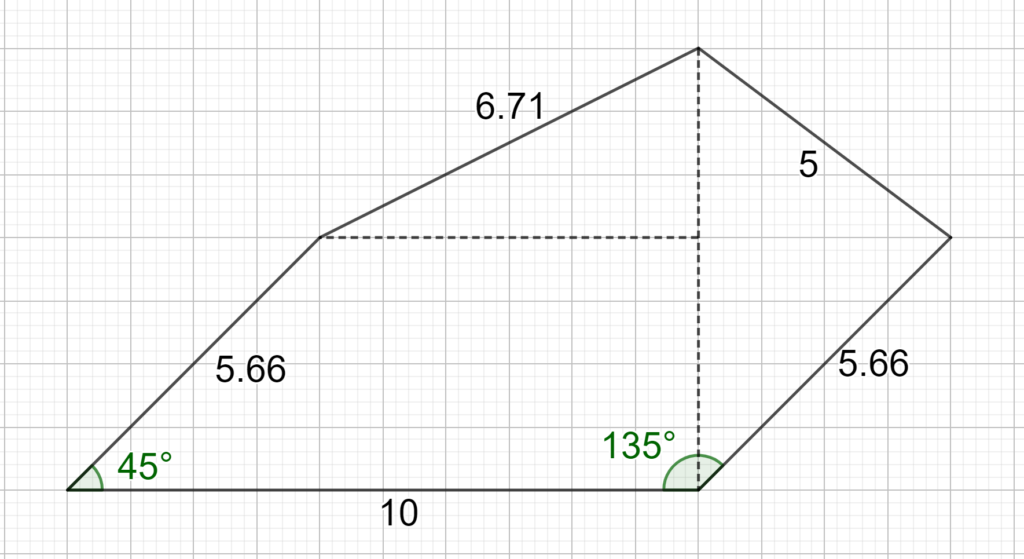
Auftrag 1:
Übertrage die Fläche in Deinen Hefter, finde mehrere Wege, diese Fläche zu zerlegen und berechne dann mithilfe der Zerlegung den Flächeninhalt.
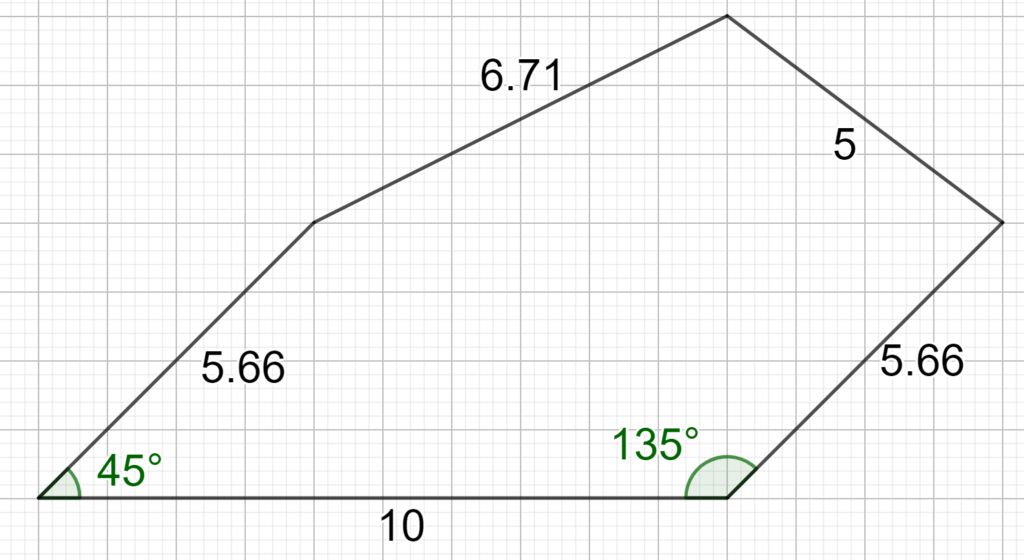
Lösungshinweise zu dieser Aufgabe (bitte aufklappen)
Diese Zerlegungen sind möglich, um die Fläche des Fünfecks zu berechnen. Miss falls nötig die fehlenden Strecken.
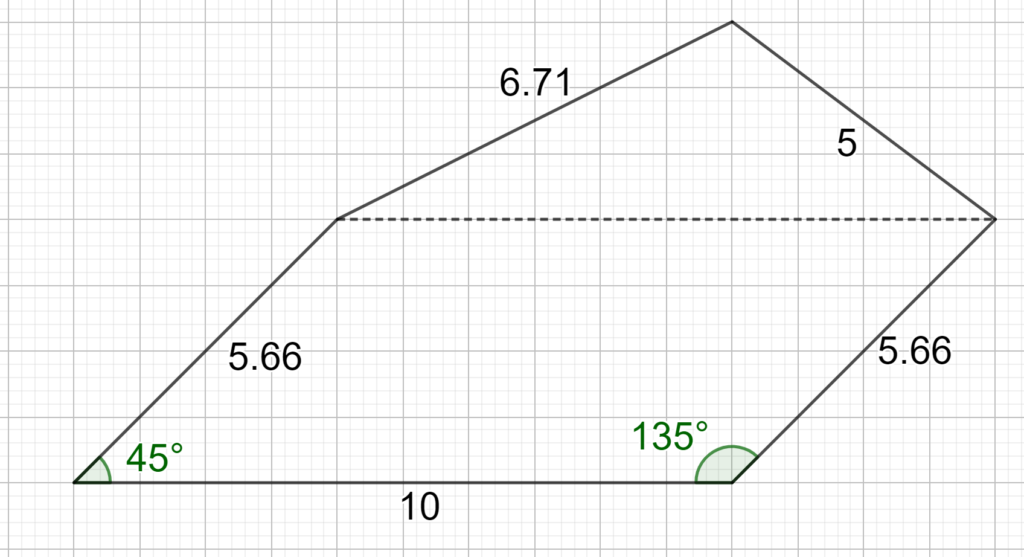
11) vermischte Übungsaufgaben
*** Hier kommen noch Aufgaben hin ***
12) Vertiefungsaufgabe: gleiche Größe?
Ich behaupte, dass die die folgenden jeweils drei Flächen alle gleich groß sind. Prüfe das nach, indem Du Die Flächen berechnest und erkläre es mit anschließend, indem Du mithilfe der Formen erläuterst, warum diese alle gleichgroß sind.
| Zeige, dass das Quadrat 5, das Parallelogramm 2 und das Rechteck 4 den gleichen Flächeninhalt haben. Natürlich kannst Du das nachmessen und rechnen, aber vielleicht kannst Du es auch anders beweisen … | Zeige, dass das Quadrat 6, das Parallelogramm 3 und das Rechteck 5 den gleichen Flächeninhalt haben. Natürlich kannst Du das nachmessen und rechnen, aber vielleicht kannst Du es auch anders beweisen … |
Diese Grundlagen bilden das Fundament für einen Beweis zum Satz des Pythagoras. Dabei handelt es isch um den sogenannten Verschiebebeweis.
![]()