Beweise spielen eine Zentrale Bedeutung beim Erkenntnisgewinn in der Mathematik. Diese unterscheiden sich vom ungangssprachlichen Beweis deutlich, da sie ein rein tehoretisches Konstrukt sind und damit quasie sinnbildlich für reine Mathematik stehen.
Befasst man sich einmal näher mit einem Beweis, so kann erkennt man deren ganze Schönheit.
Hier möchte ich einmal einen Buchtipp loswerden: Fermats letzter Satz: Die abenteuerliche Geschichte eines mathematischen Rätsels
1) Was ist ein Beweis – Nebenwinkel und Scheitelwinkel
An diesen beiden Winkelsätzen erkennt man gut, wie BEweise aufeinander aufbauen. Schaffst Du es, selbst den ersten Beweis zu finden?
Was ist denn überhaupt ein Beweis?
Vom Nebenwinkel zum Scheitelwinkel
Schaue nach, ob Du es geschafft hast, den Beweis selbst zu finden!
2) Stufenwinkel und Wechselwinkel
Nun müsst Ihr einmal selbst anfangen, die Beweise zu finden. Ihr bekommt für jeden Beweis ein Aufgabenblatt und auch Tippkarten, deren Farbe anzeigt, auf welcher Stufe der Hilfe Ihr seid. Die Hilfe nimmt immer weiter zu, die rote Karte zeigt am Ende die Lösung. (Grün – Blau – Gelb – Rot)
der Stufenwinkel
Lösungen Stufenwinkel (klicken)
der Wechselwinkel
Lösungen Wechselwinkel (klicken)
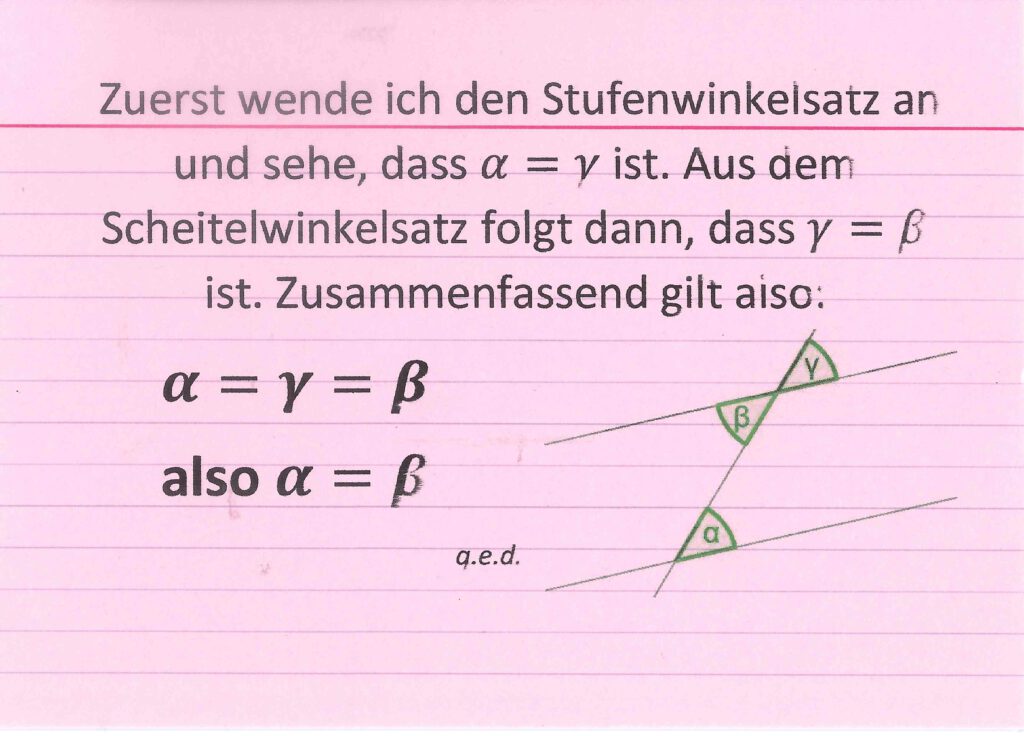
ein weiterer Winkel
Lösung weiterer Satz (bitte klicken)
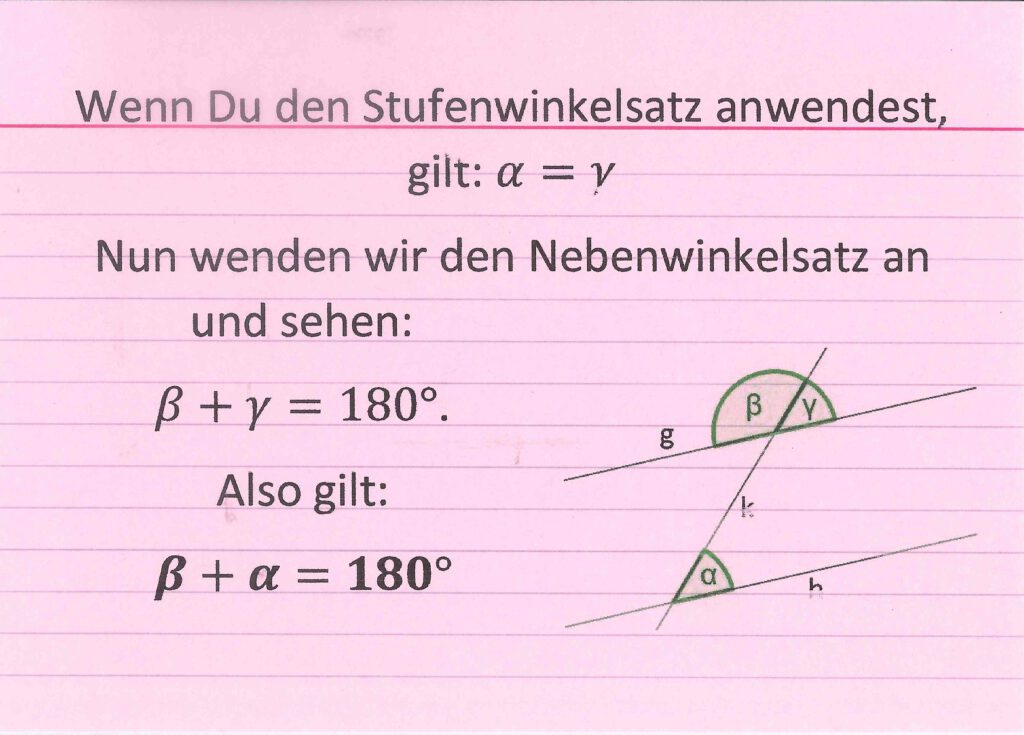
3) Innenwinkelsumme eines Dreiecks
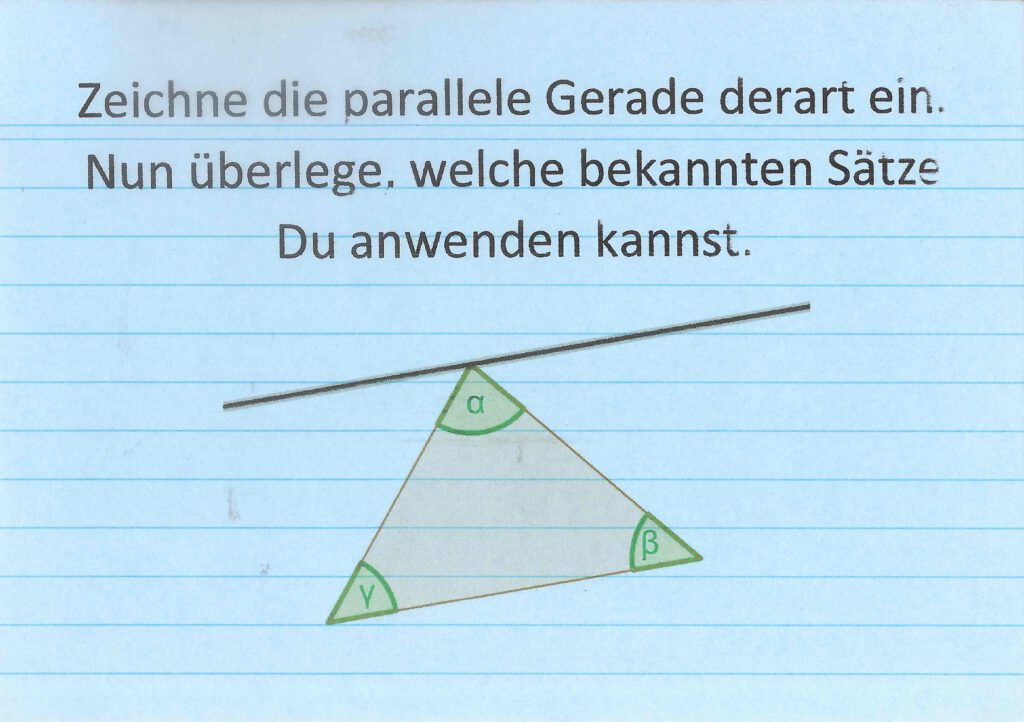
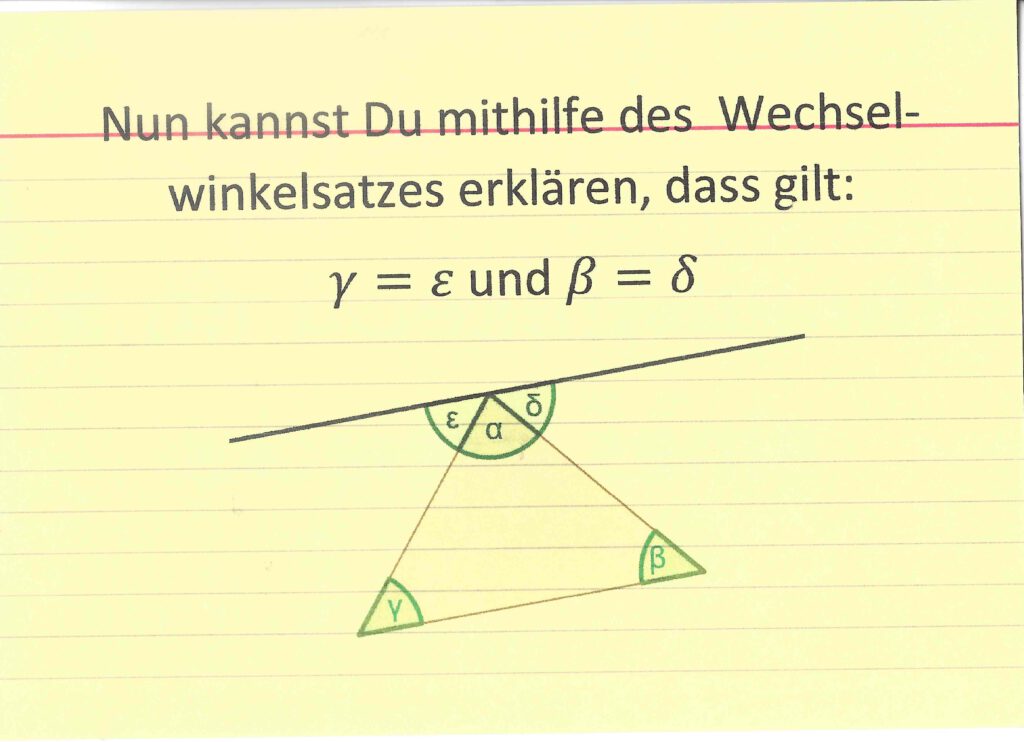
Nun beweisen wir gemeinsam, warum die Innenwinkelsumme eines beliebigen Dreiecks immer 180° sein muss.
Lösung Beweis Innenwinkelsumme eines Dreiecks (klicken)
4) Innenwinkelsumme eines Vierecks
5) Übungen … Übungen … Übungen
Hier eine Partnerübung, um sich gegenseitig zu prüfen. Nimm Dir einen Partner, löstgetrennt die beiden Aufgabenblätter (es sind nciht die gleichen) und stellt Euch die Lösungen gegenseitig vor. Kontrolliert Euch.
Formuliert anschließend beide Beweise aus.
