Nun steht Dein Abitur vielleicht schon bald an und Du möchtest Dir noch einmal im Schnelldurchlauf Infos zu ganzrationalen Funktionen beschaffen – willkommen, hier bist Du richtig.
Anhand eines Bungee-Sprunges fasse ich den Bereich „ganzrationale Funktionen“ anschaulich und umfassend zusammen und bemühe mich am Ende, einige wirklich komplexe AUfgaben zu konstruieren, die Du als eigentliche Abiturvorbereitung nutzen kannst. Aber neben dem schriftlichen Abitur helfen die Erläuterungen auch beim mündlcihen Abitur, DU kannst Dir Ansätze anschauen und selber versuchen, meine Videos nachzuspielen.
Während meines Referendariats in Bochum habe ich diesen Kontext einmal in einem Unterrichtsbesuch verwendet und erinnere mcih heute noch dran, weil das Thema dort gut angenommen wurde – und es meine beste Stunde war, die ich jemald gezeigt habe.
Ich nutze den GTR von TI (nspire). In Zukunft werde ich auch eine Version für den CAS erstellen – wenn wir diesen bei uns eingeführt haben. Aber das dauert ja noch eine Weile …
1) Der Bungee-Sprung
Eine gute Freundin hat mir ein Video ihres Bungee-Sprunges zur Verfügung gestellt, das ich im Laufe der Reihe immer wieder verwenden werde, um einige Inhalte besser verdeutlichen zu können. Schaut Euch einmal an, warum ich mich für den Kontext „Bungee-Sprung“ entschieden habe.
2) Wann bin ich wie hoch? – Umgang mit Funktionen, Werten und Stellen
Wie hoch ist denn die Süpringerin nach 2 Sekungen, wann hat sie die Höhe von 20m erreicht? Zum Beginn widmen wir uns diesen grundlegenden Fragen zum Umgang mit Sachkontexten.
Alle Lösungen zum Arbeitsblatt findest Du in den nächsten beiden Videos!
Und dann noch ein kleines Video zum graphischen Arbeiten mit dem GTR.
2a) HMF: Funktionen, Werte und Stellen, Symmetrie & Grenzwerte
Im Hilfsmittelfreien Aufgabenteil kommt es vor allem auf Rechentaktiken und Rechenstrategien an – und natürlich auch darauf, mit Brüchen, Kommazahlen und anderen ganzen Zahlen richtig rechnen zu können. Daher gibt es nun eine Zusammenfassung verschiedenster Rechentechniken, die alle für den hilfsmittelfreien Teil sinnvoll sind.
Zahlen in Funktionen einsetzen und Funktionen lösen
In diesem Arbeitsblatt mit urzer Erklärung zu Beginn findest Du Übungen zu grundlegenden Rechentechniken. Setze Zahlen in gegebene Funktionen ein und arbeite mit Quadraten und anderen Exponenten. Lösungen zu allen Aufgaben findest Du auf dem Arbeitsblatt.
Um ein bisschen fitter zu bleiben möchte ich noch auf meine kopfrechen-Übungsseite verweisen, bei der man das kleine Einmaleins (also nichts für Dich) aber auch Multiplikationen bis 20*20 üben kann … machs doch einfach mal!
Umgang mit Bruchzahlen
Hier siehst Du noch einmal kurz Rechentechniken zu Brüchen, um diese anschließend noch einmal einzuüben.
Natürlich hätte ich hier viele Aufgaben abschreiben können … aber das haben andere ja schon oft genug gemacht … hier ein Link (oder vielleicht auch mehrere, wenn ich noch mehrgefunden habe):
Und dann noch meine kleinen Programme zur Bruchrechnung:
Symmetrie & Grenzwerte
Wie war das denn noch einmal mit der Symmetrie?!?
Und dann noch ein paar informationen zum Thema Grenzwerte.
3) Wann bin ich am Wasser? – Nullstellen & verschiedene Rechenverfahren
Im Video sehr Ihr, dass die Springerin irgendwann das Wasser mit den Händen berührt. Es soll berechnet werden, wie lange dies seit dem Absprung gedauert hat, wann die Springerin in 10m Höhe ist , … dazu brauchst Du nun den GTR oder den CAS.
Um diese Rechnungen zu lösen, benötigst Du am besten den GTR. Nutze diesen auch wann immer möglich, damit Du in der Abiturklausur genug Zeit hast, um die wirklich schwierigen Probleme zu bearbeiten.
Du kannst die gesuchten Größen mit einem GTR auch graphisch bestimmen, ich lege auch diese Art der Bestimmung aber weniger Wert, da häufig rechnerische Wege gefragt werden. Auf dieses Video habe ich bereits einmal im vorherigen Kapitel verlinkt.
3a) HMF: Händische Verfahren zum Lösen von Gleichungen
Fürs Abitur benötigt Ihr ein paar Verfahren zur Lösung von Gleichungen. Schaut Euch erst einmal an, wie diese genau heißen und für welche Gleichungstypen Ihr welches Lösungsverfahren nutzen müsst.
Anschließend stelle ich Euch alle Lösungsverfahren in Ruhe vor – mit einem Fokus auf „Sonderfälle“, damit Ihr davon nicht verwirrt werdet.
Lösen durch Umformen
Lösen mit der PQ-Formel
Lösen durch ausklammern (faktorisieren)
Lösen durch Substitution
Lösen einer Gleichung mit dem GTR
Und nun zur Übung ein Arbeitsblatt mit unglaublich vielen Gleichungen, denen Ihr erst einmal ein Lösungsverfahren zuordnen müsst und die Ihr dann lösen könnt.
*** Hier kommt ein AB hin***
Teste Dein Wissen in diesem Quizz.
***Hier kommt ein Quizz hin***
4) Wie schnell fällt man beim Sprung – die Bedeutung der Ableitung und des Differenzenquotienten
Bisher haben wir eine Funktion genutzt, bei der die Höhe in Abhängigkeit von der Zeit genutzt wird. Man kann aber auch die Geschwindigkeit während eines Sprunges bestimmen und mit dieser den Sprung beschreiben.
Die Lösungen zu diesem Arbeitsblatt findest Du hier.
5) Die tiefste und die höchste Stelle – relative Extremwerte (und auch maximale Extremwerte)
Wie tief taucht die Springerin denn ins Wasser ein? Klar, das kann man irgendwie am Graphen ablesen, aber sicherlich auch genau berechnen. Dazu benötigst Du das Verfahren zur Bestimmung der relativen Extremwerte.
Auf dem Arbeitsblatt findest Du noch eine zweite Übungsaufgabe, hier ist deren Lösung:
*****Lösung noch einfügen****
Exkurs: Sattelpunkte
Beim Berechnen der relativen Extremwerte bekommst Du es manchmal mit Sattelpunkten zu tun. Zuerst hältst Du diesen für einen Extremwert, eigentlich ist ein Sattelpunkt aber gar keiner. Ich zeige Dir anhand eines Beispiels, wie Du mit Sattelpunkten umgehen kannst.
Exkurs: Bedeutung der zweiten Ableitung
Die zweite ABleitung benutzt man zum Bestimmen von Extremwerten und Wendestellen. Diese hat aber auch darüber hinausgehende Bedeutungen, die ich Dir einmal zeigen will.
***Video Bedeutung zweite Ableitung***
5a) HMF: Extremwerte berechnen
Relative Extrema kommen sicherlich auch im hilfsmittelfreien Aufgabenteil vor – daher lohnt die Übung sicherlich!
6) Wann fällt bzw. steigt die Springerin am schnellsten? – Wendestellen
Über die Geschwindigkeit der Springerin haben wir uns ja schon einmal unterhalten. Zuerst wird sie immer schneller und dann, wenn das Bungee-Seil den Fall bremst wird sie wieder langsamer. Zwischen Absprung und Wasser gibt es also eine Stelle, an der die GEschwindigkeit maximal ist – also der Fall am schnellsten ist. Diese Stelle möcjte ich nun finden.
6a) HMF: Wendestellen berechnen
Wendestellen kommen auch gerne im hilfsmittelfreien Aufgabenteil dran, also schaut Euch das mal an hier.
7) Ränder der Modellierung
Wir haben die Funktion f, die wir zur Beschreibung des Sprunges genutzt haben, gewählt, weil diese einige Eigenschaften des beobachteten Sprunges relativ gut beschreibt. Im Detail weicht die gewählte Funktion vom tatsächlichen Sprungverlauf etwas ab. Eine Abweichung haben wir durch den Definitionsbereich bereits ausgeschlossen – da die Funktion die Höhe der Springerin vor x=0 und nach x=5 nicht mehr beschreiben kann. Diese Ränder der Funktion müssen aber berücksichtigt werden.
8) knickfreie Übergänge
Dieser Abschnitt wäre etwas „an den Haaren herbeigezogen“, wenn ich diesen auch auf den Bungee-Sprung beziehen würde. In anderen Zusammenhängen kann diese Methodik aber durchaus sinnvoll genutzt werden.
*** Hier kommt ein Video hin ***
8a) HMF: Tangenten berechnen
Wendetangenten werden auch gerne im hilfsmittelfreien Teil einer Klausur berechnet, weil es recht einfach aber doch irgendwie komplex ist. Legt doch mal los!
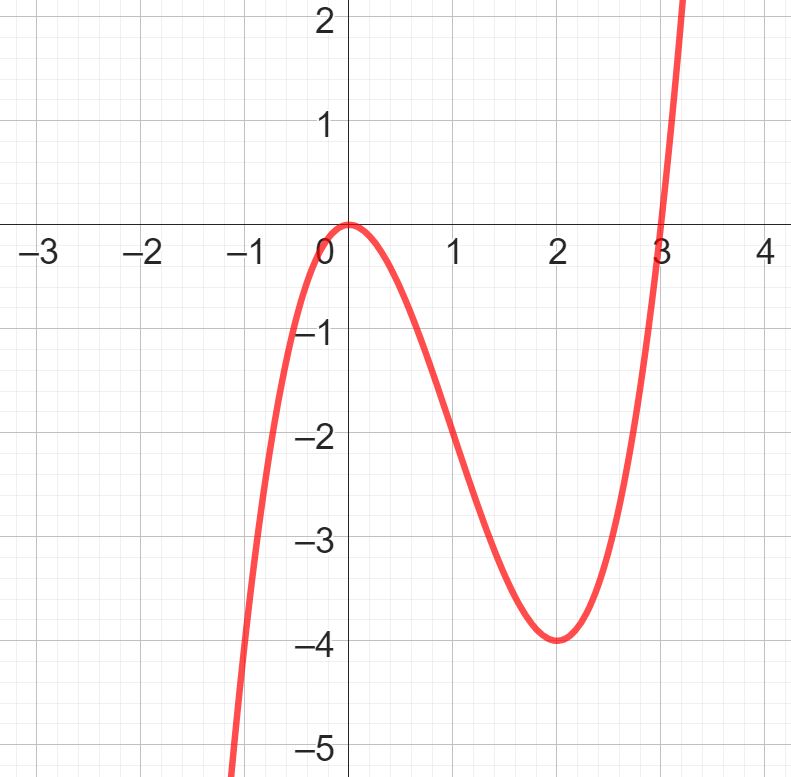
Aufgabe: Bestimme die Nullstellen der Wendetangente dieser Funktion vierten Gerades mit der Funktionsgleichung .
Überlege Dir erst einmal, was alles nötig ist um diese Aufgabe zu lösen und fange dann an. Alles findest Du im Video.
9) ein anderer Ansatz: Vertikalgeschwindigkeit anstatt der Höhe
Bisher sind wir davon ausgegangen, dass wir die Höhe der Springerin in ABhängigkeit von der Zeit gegeben haben. Dieser Ansatz ist sicherlichsinnvoll und führt zu einem guten Ergebnis.
Technisch ist es aber häufig auch so, dass man nicht die aktuelle Höhe in Abhängigkeit von der Zeit gegeben hat, sondern dass man die aktuelle Geschwindigkeit in Abhängigkeit von der Zeit als Basis-Messgröße gegeben hat. In der Messtechnik kommt so etwas sicherlich häufiger vor, da man Geschwindigkeiten technisch recht leicht messen kann.
Für die nächsten Absätze nutzen wir also die Funktion v(x), die die aktuelle Geschwindigkeit in ABhängigkeit von der Zeit angibt. Selbstverständlich kennen wir die Funktion v bereits, denn das ist ja die Ableitung der bisher genutzte Funktion f.
***video***
9) Wann ist der Springer in welcher Höhe – mithilfe der Integralrechnung
9a) HMF: Flächen unter Funktionen
10) Wie verläuft der Bungee-Sprung – mithilfe der Vertikalgeschwindigkeit
11) Grenzen bei Integralen bestimmen
11a) HMF: Grenzen bei Integralen ausrechnen
12) Vergleich dreier Sprünge – Funktionen verschieben und umformen (auch HMF)
Bungee-Sprünge ähneln sich nicht wie „ein Ei dem anderen“. Es gibt verschiedene Größen, die Einfluss auf den Sprung haben.
- Die Höhe, in der der Absprung stattfindet
- Die Länge des Gummibandes zum Abbremsen
- Die „Härte“ des Gummibandes zum Abbremsen
13) Wann ist der Höhenunterschied zwischen zwei Springern am größten? Wann gleich Null? – Vertiefung mit zwei Funktionen
Hat man nicht nur eine Funktion sondern auch eine andere, so kann man diese miteinander vergleichen … schauen wir doch mal.
14) Flächen zwischen Vertikalgeschwindigkeiten – was kann man sich darunter vorstellen
15) Durchschnitte bestimmen und interpretieren
16) Steckbriefaufgaben – Und was tun, wenn sich die Eigenschaften des Sprunges verändern?
16a) HMF: Steckbriefaufgaben lösen (auch GTR)
Steckbriefaufgaben kommen nicht immer im Sachzusammenhang vor – sondern gerne auch komplett ausserhalb desgleichen. Hier zeige ich Euch eine ganz allgemeine Einführung und anschließend zwei Aufgaben, die ich Euch ganz genau durchrechne und kommentiere. Ihr könnt natürlich auch erst einmal alleine ausprobieren, ob Ihr es schafft.
Diese beiden Aufgaben bespreche ich im folgenden.
 |  |
Steckbriefaufgabe Funktion 3. Gerades
Steckbriefaufgabe Funktion 4. Gerades
17) HMF: Der Gauss-Algorithmus
Den Gauß-Algorithmus haben wir bereits einmal bei der linearen Algebra eingeführt – man braucht ihn aber auch beim Erstellen von Steckbriefaufgaben und später noch einmal in der Matrizenrechnung.
Damit es nicht zu langweilig wird, hier noch ein paar Übungen. Übungen findet man im Internet und in jedem Mathebuch zu Hauf.
Auf dem Arbeitsblatt befinden sich schon QR-Codes zu den Lösungen – aber hier gibts die Links noch einmal extra.
18) Wir verändern den Sprung – Funktionsscharen
Funktionsscharen sind eine Erweiterung der klassischen Funktion. Die klassische Funktion hängt von einem Wert (der sogenannten Variablen) ab – diesen bezeichnen wir in der Regel als X-Wert – manchmal auch als t-Wert. Nun kann man einer Funktion aber noch weitere veränderliche Größen hinzufügen – sogenannte Parameter. Ein Parameter wird klassischerweise mit einem kleinen Buchstaben in der Funktion dargestellt – meist nutzt man ein kleines a. Dieser Parameter hat Einfluss auf den VErlauf der Funktion. Er ist aber – im Gegensatz zur Variablen – für einen Funktionsgrapen immer konstant. Man kann also einen Funktionsgraphen für z.B. a=1 zeichnen, einen weiteren für a=2 …
Schauen wir mal, welchen Einfluss so ein Parameter auf den Verlauf unseres Sprunges hat.
Die Erklärung folgt sogleich.
Mithilfe des GTRs lassen sich Funktionsscharen wirklich gut bearbeiten – wen man denn weiß wie.
*** Hier kommen noch Übungsaufgaben hin ***
18a) HMF: Funktionsscharen
Funktionsscharen kommen gerne im hilfsmittelfreien Aufgabenteil vor, da man damit gut zeigen kann, wie gut – oder eben nicht – man rechnen kann. Nimm Dir die gegebene Funktionsschar und versuche, damit die Nullstellen, die Extremwerte, die Wendestellen und das Integral zu berechnen.
277 total views , 1 views today